s₀からs₁までの光学的厚さτ の気層があって、s₀から放射された波数範囲ν +Δν の放射がs₁で観測される強さは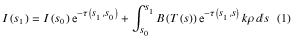
と表される。また、

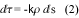
ここで、k は吸収係数（extinction coefficient）であり、透過率Tr=e^-τとすると、
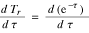であるから、
dTr = - e^-τ dτとなり、(2)式から
dTr = e^-τk ρ ds となる。従って(1)式は、Tr を用いて、

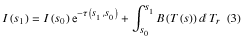
と表される。あるいは、地表からの放射伝達を考慮して、

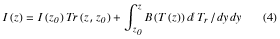
と表される。ここに y=- ln p であり、dTr/dy は重み関数である。(3)式を離散的表現に直せば、

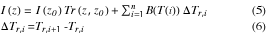
なんで、わざわざ展開したのかと言えば、普通は最初の式と最後の式しか与えられておらず、いわば気持ち悪いから、という理由に過ぎない。

上の最後の式の通りに計算すればモデルの出来上がりなのだが、実は、計算速度の関係で悩ましいところがある。実はFourier空間上の吸収係数計算のステージにおいては、一番計算コストのかかるInterferogram関数（現実のFTSのInterferogramと異なるが便宜上こう呼ぶ）の計算の時に適当な窓関数をかけて計算を途中で打ち切る、つまり０にしてしまうことによって、計算する波数分解能を下げて計算時間を短縮することができる。

ところが現実の大気をFTSで観測する時、観測結果S_ftsの波数分解能は Br Tr にかかる装置関数 f* によって決定される、つまりS_fts= f* ⊗ (Br Tr) として表される（Br は放射 Tr は透過率）ので、計算時間短縮のためにInterferogram関数で分解能を下げるた結果は、実際のFTSによる測定結果と異なる結果となる。 Br の波数方向の変化率はFTSの分解能を考えると無視できるほど小さいから、これを無視して
(1) S_fts= f* ⊗ Tr 、書き換えると
(2) S_fts= f* ⊗ exp(- τ)、さらに書き換えて
(3) S_fts= f* ⊗ exp(- ρ k*) 、となる。

つまりモデル計算におけるInterferogram関数を f'とし、モデル計算の結果をS_mとした時、ρ は一定であるから無視するとして、
(4) S_fts= f* ⊗ exp(- k*) と
(5) S_m= exp(- f*' ⊗k*) の違いはどの程度あるかを調べておく必要があるのだ。どの程度というのは、あまり違いはないだろうという予測があるからだ。
これをFourier変換F を用いて表せば、 k*, f*, f*' のフーリエ変換型を k, f, f'とした時、

(6) S_fts=F{ f·F*( exp(- k*) ) }
(7) S_m= exp( -F{ f'·k } )　となる。次に両式のexp を０のまわりに級数展開すると（Tr ≈ 1= exp(0) だからそうおかしな近似にはならないと思われる）、

(8) S_m= 1 -F{ f'·k }+ F{ f' · k }²/2- F{ f'·k }³/6+ O
(9) S_fts=F{ f·F*( 1- k*+ k*²/2- k*³/6+ O) }　となり、Fourier変換を実行して、
(10) S_fts=F{ f· (δ- F*(k*)+ F*(k*²/2)- F*(k*³/6)+ O) }　、さらに
(11) S_fts=F{ f·δ- f·k+ f·F*(k*²/2)- f·F*(k*³/6)+ O }
(12) S_fts=F(f·δ)- F(f·k)+ F(f·F*(k*²/2))- F(f·F*(k*³/6))+ O

(8)式と(12)式の各項を比べると、第一項の常数項を無視すると、第二項は等しい。問題は第三項以降をどう評価するかにあると思われる。ぱっとみでは、F{ f' · k }²/2 とF(f·F*(k*²/2)) のf について(8)式の方が二乗になっているので、f の効き方がよい、つまり高周波成分が早く落ちると思われる。簡単に考えれば、モデル計算の方は少し余分に計算しておいて、Tr を出してからもう一度フーリエ変換して装置関数をかけてから、逆フーリエで戻すという格好になると思われる。実際には計算して効きの具合を確かめる必要があるだろう。

上の話をどんなふうに実際に数値計算を行うかといえば、
(1) 適当な化学種と波数域を選ぶ
　以前計算したことのある条件で、O₃あたりを選ぶがよかろう。FASCODと比較済みの波数域だ。Rと呼ぶ
(2) 適当な装置関数、例えばNorton-Beerの関数なんぞで、上の計算結果に装置関数の畳込みを行う。
(3) L2FTV（モデル計算）のInterferogram関数を遮断波数を高周波数側から徐々に動かして、Rと比較する。
最初の比較は偏差のトータルの変化を遮断周波数でみてみるか。Norton-Beer関数で遮断周波数のようなパラメータを決定できたかどうか？
Norton-Beer関数を見直してみると、
c0 = 0.26;
c1 = -0.154838;
c2 = 0.894838;
apodizN := c0 + c1(1 - U²) + c2(1 - U²)² 、（U: normalized path difference, 0≤U≤1）という関数型でBeerはこれを"weak apodization"と呼んでいる。

pass difference がキーになるかも知れない。モデル計算は最終的には実機に適用されるし、よく見るとN-Beer関数がU=1に向かって漸近的に、０にならずにある程度なだらかに小さくなって、ストンと０になる、というのは実際のinterferogram、即ち装置関数の係った後の干渉波形に近い形を想定しているものと思われる。

今回の場合もpass differenceの何倍あたりまで多めに計算しておくか、という指標のつけ方がよさそうに思える。つまり、モデルはpass differenceを要求し、その後に装置関数はどれが一番実機に近いかをユーザが選択する、という手順となるだろう。この辺りはFASCODのパラメータ設定においてもしっかりとした認識が示されていないようだ。

* N.H. Norton and R. Beer, New apodizing functions for Fourier spectrometry, J. Opt. Soc. Am., Vol. 66, No. 3, 1976, 259-264.
p.s. ところで、apodization function とinstrument function は片やフーリエ空間上、片や波数空間上で同じものを表しているのだが、ここに詳しい。これもWolframのページで、いつももやもやしていたものがMathematica ではっきりとさせる、というパターンに思われる。

取り合えず、期末に千葉大学の要求である、成果発表会のポスターが作れる程度にまとめる必要はある。

改めて書類を引っくり返してみたら、受託研究ではなくで、旅費は大学から直接に、消耗品は大学内の担当教官が発注してこれを受け取る、という形式であることが分った。

現実の話、担当教官にいきなり発注してくれ、と頼んで買ってくれる筈もないから、まず秘書がだれかを探して、次に秘書が購買業務をこなすかどうかを確かめなければいけない。直ぐに指定した品物が入るとは限らないので何回かやり取りして、業者からの連絡後、受け取り、検収、重量物であったら大学からこちらへ輸送、なんてことを考えると現実的に実行できるとは思えない。

先生に適当に使ってくれ、と言うしかないような気がする。おまけに12月中に消耗品の購入を含め作業を終了させなくてはいけないことも分った。(2003.9.11)

11月の末にはタイに行かねばならない。帰ってきたらもう暮れの25日だから、仕事は何にもできまい。早くこの結果をまとめてポスターにして、今年度の本来の研究の仕上げにかからなきゃいけない、と段々、尻に火が近づいてきた。これにとっかかる前に政策研の月報を仕上げなきゃいけなかったし、タイの準備もしなきゃいけなかったので、全部が玉突き状態になっていたのだった。おまけにADEOS-IIがトラブルで停止したものだから、11月の始めは殆どそれにかかりっきりになってしまって、増々予定が遅れた。

そんな訳で、取りあえずADEOS-IIのトラブル対応は一週間で主なところに方をつけた。タイ用の準備資料は最新の電力事情データにアップデートしてハンドアウトを作り、OHPを準備した。政策研の月報は11月の第一週金曜までで、桑原所長のご意見を伺いながら仕上げた。で、やっとここに戻ってきたわけだ。

まず、全体の流れを整理した図を作った。ポスターにも転用ができるようにだ。

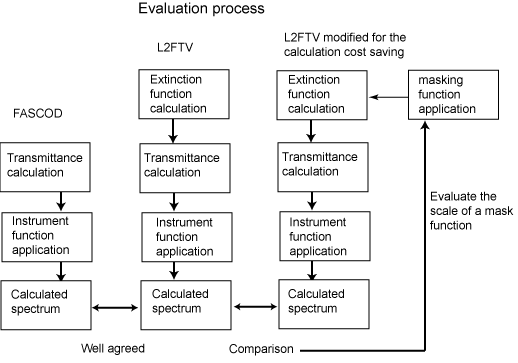
最初に装置関数を選ぶ。予定とおりNorton-Beerとした。窓の幅なんだが、かなり狭くしないと目に見えるような分解能の低下を得ることができない。適当にサイズを選んだのが、下の関数だ。

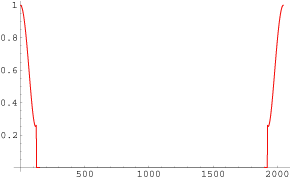
つきあたった問題が、この窓の幅はどのように定義すればよいか、という点だ。対称形になっていることを考慮して、124/1024= 0.121、これをeffective width と呼ぶことにする。この装置関数を畳み込んで得られたスペクトルが、

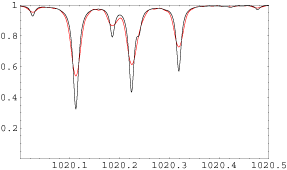
の赤線のスペクトルだ。黒線が元のL２FTVスペクトル。

こうして、準備が整ったので、吸収係数を計算するところで矩形のmask functionをかける。この時、計算は2048点の長さについて行っているので、mask function のeffective width は、maskの長さ/2048とする。こうしておいて、maskの長さをあれこれ変化させてから、元のスペクトルとの差のrmsを求めた結果が下図だ。

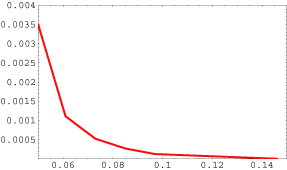
大雑把にみて、instrument function の幅程度のrectangular mask function で誤差は十分に小さくなることがわかる。こうするとバンドモデルや、ILAS-IIの計算のように分解能が非常に低い場合、mask function の幅も非常に小さくできて、殆ど計算時間を要しないようになるのではないか。
もちろん、黒体放射の波長特性を無視した場合にこう言えるのだが。逆に黒体放射の波長特性を近似してやればよいのではないか、とも思われる。

結果が出たので、とりまとめてから、ポスターを製作することとした。今まではプロッタ／プリンタがなかったので、外注していたのだが、外注だと時間がかかる。データセンターに大型のプロッタ／プリンタが入っていたのは気付いていたので、これを使うことにした。こいつも、現場の意見としてはHPのPS付きのを最初に要望していた筈なのに、いつのまにかEpsonになってしまっていた。安くて大判のものが印刷できるというので、Winしか使ったことがない、PSなんかに無頓着な輩が選んでしまったに違いない。

使わにゃ仕方がないので、調べると133.187.108.153、EpsonのPM10000で、たまたまMac-Xの10.3を入れてあったので、CUPS+GIMP-print が使えるようになっていてよかった。プリンタ追加を選んでIPプリンタにLPD/LPRコマンドを出すような設定にすればよいのだ。10.3より前だったら使えなかったところだ。

機種を選んだ奴に腹をたてても仕様がない。Illustratorからすんなりとプリントすることができた。ここらあたりLinuxなんかでは相当に苦労するだろうと思われる。

いろいろ準備が進んだので、今度は放射輝度のJacobian の計算プロセスを定式化したい。実にうまいことに、ある関数f の微分はスペクトル空間ではF (2pit)^n dt というような実に簡単化された形式で表現されるからだ。

なんて思い付きを書いてみたが、一寸考えると波数方向の微分でななくて、濃度方向の微分だったので、これでは明後日の話をしてしまった。思い付きでなく、Jacobianをどうするのかしっかり考える必要があろう。