IMGのような直下視センサで対流圏のCO2が、測定可能であるかという問いに対して、確かに我々は答えてこなかった。一つにはCO2をターゲットにすることに対するリスクが大きかったこと。つまり、内外研究者のIMGセンサに対する理解がその時点では十分とは言えず、仮にCO2が可能であると宣言することは、そのバリデーションを我々自身が実施しなければならないことと等しく、研究リスクが高すぎたと考えたためである。
とは言え、IMGセンサのソフト側のFSにおいては、リトリーバルのシミュレーションを行い、統計的にCO2濃度が鉛直方向に3層の分解能を与えた時2%の誤差で取得できることを示した。CO2温度が高い相関を持っているにも係わらず、気温とCO2が分離できる要因として、気温がCO2のみならず例えばH2Oとも相関を持つ、即ち、気温のリトリーバルがH2Oの波長域でも可能であるため、CO2と気温が分離できることをその根拠としてきた。
一方、近年になってCO2センサの必要性が高く叫ばれるようになって、IMGが真にCO2観測ができることを広く示す必要が生じてきた。2002年度ATRASグループでは、富士総研に委託して、IMGセンサの感度解析を再度行った。計算コードにLBLRTMv6.12、吸収線データとしてHITRAN2000を用い、大気を18層に分けて(0〜15 kmまで1 km刻み、および20 kmと40 km以上)、波数分解能0.1 cm-1の条件において、対象大気成分を一つずつ、各気層ごとに変化させて、宇宙空間から観測した場合の放射量変化を計算した。対象大気成分は以下の通りである(括弧内の数字は変化させた量である)。
温度(1K)、H2O(10%)、CO2(10%)、O3(10%)、CO(10%)、CH4(10%)
この時、できるだけ現実大気に近い条件で感度解析を行うという観点から、大気の気温・水蒸気分布、および地表面温度データとして、NCEPreanalysisの1997年から抽出し、これを緯度別に5つのパターンに分類したものを使用している。
計算結果から、CO2と温度が果たして分離してリトリーブできるか否かを見るために、波数ー高度断面における、それぞれの変化率の等値線を描いてみた。即ち、等値線が0の部分はCO2/温度の変化に対して衛星から観測しても変化の認められない部分であり、それ以外が変化の観測できる領域である。もし、この領域の位置に、CO2と温度との違いが存在する場合、我々は、この両者を衛星観測から分離できるとする十分な理由がある。
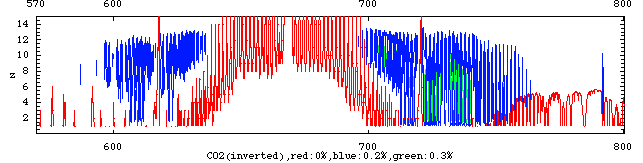
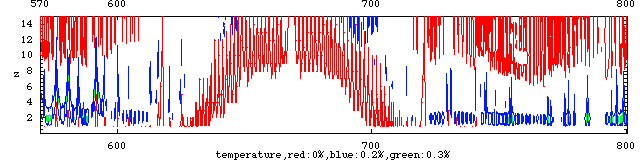
上図がCO2について、下図が温度についての解析結果である。この時、両者はその変化の傾向が逆であるため、つまり、CO2が増加すると温度は下がるため、CO2の変化率については-1をかけてある。
図から、明らかに両者の変化率の異なる領域が存在する、即ち、衛星観測から、温度とCO2の両方を同時にリトリーブできることが結論できる。また、この時の変化率0.2%はS/Nに換算すれば概略500であり、IMGにおいても既に達成されており、ただ一回の測定であっても、CO2の10%の変化に対して感度のあることが判る。
topマイケルソン型干渉計のS/N計算式というのはなかなか見つからないのだが、IMGの時の計算式があったので、参考のために書いておくことにした。
(eq.1) 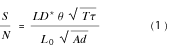
ここで
| L | : radiance | ; (3) | W/(cm2 Sr cm-1) |
| D* | : detector detectivity (wave-n <2000 cm-1) | ; (1010) | cm Hz ½ /W |
| : detector detectivity (wave-n >2000 cm-1) | ; (1011) | cm Hz ½ /W | |
| Θ | : system throughput | ; (0.015) | cm2 Sr |
| T | : dwell time | ; (10) | sec |
| τ | : system efficiency | ; (0.1) | cm2 Sr |
| L0 | : total optical path difference | ; (10) | cm |
| Ad | : detector area | ; (0.017) | cm2 |
システムスループットΘ は、
(eq.2) Θ = 2πAΔκ/MAXκ
ここで
| A | : area of interferometer mirror | ; (π52) | cm2 |
| Δκ | : spectral resolution | ; (0.1) | cm-1 |
| MAXκ | : maximum wave number | ; (3300) | cm-1 |
(eq.3) Ad= FΘ/ A
ここで
F : forcal length ; (30) cm (f=3)
上のパラメータの括弧の中の数値はIMGの値である。この値を用いるとIMGの場合のS/Nは、
| Wave.n(cm-1) | 300K | 200K | Std.atm. |
| 718.0 | 531.2 | 91.0 | 254.7 |
| 1010.0 | 327.4 | 31.7 | 254.7 |
| 1277.0 | 200.1 | 9.1 | 47.3 |
| 1278.0 | 200.1 | 9.1 | 54.6 |
| 1590.0 | 87.3 | 1.9 | 14.6 |
N= 0.027 μW/ (cm2Sr cm-1) である。
top
IMGのリトリーバルで問題になったことの一つに、イタレーションの取り扱いがある。具体的には、逆問題を線形化して最尤法で解くのだが、その結果得られた解を初期値として、再度計算する手法、つまりイタレーションをどう考えるべきかどうか、という議論だ。適切な初期値が与えられているならば、最適な結果が得られるのが最尤法である筈なのに、実際には、イタレーションを行うと誤差が改善される、という結果が得られる。IMGの開発プロジェクトの時の経験だ。
この事実は、初期値と真値との関係に線形性があるとする仮定が十分でない、ということを示している。もちろん、この事は良く知られた事実なので、より真値に近いと思われる解を求めるために、適切な初期値を選ぶ等の対策が取られてきた。つまり、最尤法では最適解が得られないという結論が出ないように、つまり最適な手法として最尤法を採択したという論理の、破綻を避ける努力がなされてきた。だが、初期値が真値と一致することはあり得ないし、そもそも初期値が十分に真値に近いのなら、観測の必要性がなくなってしまう。つまり最尤法による非線形な逆問題の解法というのは、本質的に矛盾を含んでいるものと考えられる。
さらにイタレーションが有効である、というIMGの経験から言えば、実際には、最尤法による多くの解が最適値ではなく、局所的な最適値に「近い」値に過ぎないということが推定できる。かつ、測定値の分散により、解を初期値周りに拘束する、という条件のかかっていることを考えると、最尤法から出発したイタレーションによる解も初期値の周りに存在する確率が高いと考えられ、得られた解が大域的な最適値である、ということは言えないと思われる。
これらの問題点を緩和するためのひとつのアイデアが、遺伝アルゴリズム、GA(Genetic Algorithm)、の採用だ。基本的には解の存在可能空間をしらみつぶしに探索して最適値を得る手法だから、計算に非常に時間がかかる。だが、基本的には力技なので、計算コストが安くなってきた昨今、まじめに取り上げてもよい時期なのではないか、と考えたのが始まりだ。
取りあえずWeb で調べたら学生向けの講義資料 が見つかった。丁寧に書かれているので、私のような初心者にもよく分かった。なにせGAとGP(Genetic Programming)の違いが分からなかったぐらいなのだから。また、サンプルプログラムも見繕ってみた。その他にも資料として遺伝的プログラミング入門、伊庭斉志、東京大学出版会、2001.を買ってきた。(2004/10/20)
EORCのSzk氏からメールが来て、これにMégie のペーパーが添付されていた。C.Clerbaux, J.Hadji-Lazaro, S.Turquety1,G.Mégie, and P.-F.Coheur, "Tracegas measurements from infrared satellite for chemistry and climate applications," Atmos. Chem. Phys. Discuss., 3, 2027−2058, 2003というものだ。
中身は彼らがIASIのデータ解析アルゴリズムを開発したので、打ち上げ前のIASIの代わりにIMGのデータを使ったというものだ。読んでみると、彼らの結果はまだ出ていなくて、殆どレビューに終止しているのだが、IMGのことが詳しく紹介されている。IMGの圧倒的な性能に彼らが驚いている様子が、行間に滲みでている、と感じるのは身びいきのあまりだろうか。
IMGが逝ってしまって7年、ああ生きていてくれたら、どんなに素晴らしい成果が出ていただろうか、今ならグラウンドデータも揃ってきているのに、と思うが、まさに死児の齢を数えるに等しくて、こういうペーパーを見るたび、寂寞たる思いにかすかなためいきが出る。(2004/10/25)
さてGAについては、ボチボチ進めている。最終目的は、温度と各種気体濃度のリトリーバルだからGAも多変数を扱わなくてはならない。そこで、サンプルプログラムをまずは、二変数を扱うように書き換えることとする。
できあがったのが、二変数GAサンプルプログラムで、元のプログラムからは大分書き換えてある。一つ悩ましいところがあって、Mathematica でプログラムを書く以上、Mathematica らしくしたい、つまりCスタイルのDo 文や、代入文は書かない、ということなのだが、後々でCに変換することを考えると、Cスタイルに近く記述してあった方がよい、という判断もある、どちらを選ぶかが悩ましい。どちらでもよいのだが。
実際にステップ毎に元のサンプルプログラムを動かしていくと、GAについて朧げな理解だったのが、少しは深まった。プログラムの骨格がどうなっているかと言えば、
(1)の評価累積リストの頭からランダムに子を選ぶと、評価関数の大きさで重み付けしたことになる、という点が、元のプログラムのスマートなところで、(5)の再度規格化する、というのが同じくそのミソのようだ。
というわけで、下の図が、順に、FitnessFunction(評価関数)、FitnessFunctionを等高線表示した上で初期化値を重ね合わせたもの、同じく20回のイタレーション後の結果だ。
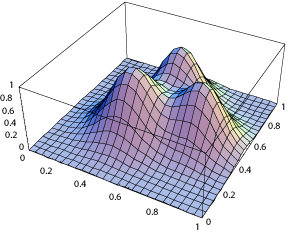
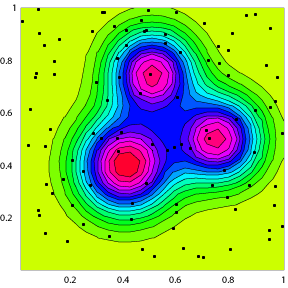
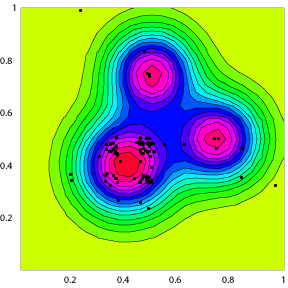
図をみれば、確かに、一様にばらついていた初期値から、最も高い山に数値群が集まってきているのがわかる。しかし、必ずしも一番高い山の頂上に集中せずに、頂上の周りに集まっているようにもみえる。なぜ、頂上に集中しないか、というのは、突然変異の与え方や、遺伝子交換の方法、評価リストの規格化の影響と思われるのだが、まだ、調べていない。(2004/11/17)
GOSATの行く先は明らかでないが、かと言って手をこまねいているわけにも行かない。最初にIMGの関連報告書を集めることとした。EORC内部で探してみたが、断片的にしか残されていなかった。仕方がないので、Som氏に我孫子研まで行ってもらって、書庫から、IMGの報告書、「広モ」の平成元年度から10年度までを回収してきた。
プログラムのソースコードについては、勿論、テープに記録して残してある。だが、長い経験から言って、テープに記録されているソースコードから、そのコードが発揮していた機能を再現できるか、と言えば、一般的にかなり困難を伴う。まず、テープを読めるか、という問題があって、開発経緯から、DATと8mmに別れているのだが、ドライブを探すことから始めなければいけない。ドライブを探し出したとしても、そのドライブで読めるかどうかの問題がある。往々にして、読み取りミスを連発する。また8年近く経った磁気テープの品質が保たれているかどうか大いに怪しい。そもそも磁気テープは、年に数回の巻き直しをメインテナンス作業として求められていることが多いのだ。
幸運にもテープからソースコードが回収できたとしても、これをコンパイル&リンクできるかどうかの問題がある。しばしば必要となるサブルーチンが抜け落ちていたり、コンパイラへの指示を与えるmakeファイルが、ソースコードのファイル群の位置について正しく記述していなかったりするのは、よくあることだからだ。ライブラリやOSも違っているので、リンクエラーが、ばたばたと出るに違いない。その度にmakeファイルとソースコードの中身を、読まなければいけない事態となるのが、目に見えるようだ。
無事、リンクが完了したとしても、実行時の環境、すなわち初期値だの、テーブルだのといった、サポートファイル群が揃っているかどうか、が次の問題となる。テーブル等のサポートファイルは、バックアップとして記録されることが多いから、ソースコードとは別物として扱われている場合が多い。ソースコードを記録したテープに、その情報も入っているかどうか、というのは、殆どギャンブルで、大抵の場合こちらの思惑通りにならない。
こういう時のためにプログラム設計書がある、という人がいるだろうが、何を書いているのかよく分からないシートが分厚くファイル化されている代物から、全体像を読み取ることのできる人などいるのだろうか。そもそもプログラム設計書というのは、プログラムをコーディングする時の目安で、出来上がったプログラムを、後から理解するために、作られているのではないからだ。しかも、プログラム開発を請け負ったベンダーが、後々にプログラムを見直すため、最終のソースコードと設計書の記述をぴったり一致させておく、というようなことは殆ど期待できない。
できない、できない、と役人のようにできない理由を書き連ねてきたが、それじゃ良い方法があるのか、と言えば、どうもなさそうで、結局、一から作ったほうがよさそうに思う。
今ならどうするか、と考えれば、Mathematica でアルゴリズムと結果とテーブルと説明を全部ひとまとめにしておくのが、一番分かり易い。しかし、Wolfram社がなくなったらどうするのか、という話もあって、何をしようが、一旦サポートが途絶えてしまうと、ソフトウェアシステムを再現するのは極めて困難、という平凡かつ深刻な結果に辿り着いてしまう。 (2004/12/10)
■ ■ ■